应yl7703永利官网邀请,东北师范大学数学与统计学院扶先辉教授,兰州交通大学数学系梁力教授,江苏理工学院胡江胜教授,华侨大学朱荣民博士四位专家于10月19日早上8:00----下午6:00在腾讯会议举行线上学术报告。报告会由yl7703永利官网王永铎教授、吴徳军教授主持,永利集团、兰州交通大学、西北师范大学、东北师范大学等师生百余人参加了本次会议。
扶先辉教授做了题为:“经典逼近和理想逼近”的报告,该报告从基本概念出发,介绍理想逼近的例子、基本想法及其应用。特别地,该报告力图说明理想逼近是经典逼近的起始步。
梁力教授做了题为:“A refinement of Gorenstein flat dimension via the flat-cotorsion theory”的报告,该报告介绍了结合环上Gorenstein平坦维数的一个细化,并进一步证明了它不同于一般环上Gorenstein平坦维数,给出了无界同调和virtually Gorenstein环的一些应用。
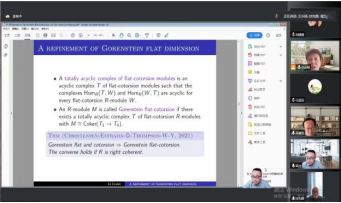
扶先辉教授做报告 梁力教授作报告
胡江胜教授做了题为:“Resolving dualities and applications to homological invariants”的报告,该报告介绍了阿丁代数上有限生成模范畴的resolving子范畴的对偶概念,建立了有限生成投射模和有限生成Gorenstein投射模的同伦范畴之间的联系并证明了高阶K群是同调不变量。
朱荣民博士做了题为:“Gluing compactly generated t-structures over stalks of affine schemes”的报告,该报告证明了交换环导出范畴里的紧生成t结构和环关于其素谱里所有极大理想的局部化后对应导出范畴里有限生成t结构之间存在双射。进一步地推广了Trlifaj和Sahinkaya等人关于环上cosilting对象的结果。
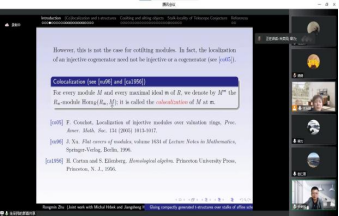
胡江胜教授作报告 朱荣民博士作报告
四位专家在分享精彩报告过程中,他们严谨的论证、渊博的知识、风趣的语言给参加本次会议的师生留下了深刻印象,师生们受益匪浅!
报告人简介:
扶先辉,东北师范大学数学与统计学院教授,研究方向为同调代数和K-理论。研究工作发表在Proc. Lond. Math. Soc.,Adv. Math.,J. Pure Appl. Algebra,J.Algebra等期刊,现主持国家自然科学基金面上项目。
梁力,兰州交通大学数学系教授,博士毕业于南京大学。主要从事同调代数与表示论的研究,研究成果发表在Trans. Amer. Math. Soc.、Israel J. Math.、J. Algebra、J. Pure Appl. Algebra、Sci. China Math.等国内外重要学术期刊上,已主持完成多项国家及省部级基金,目前主持一项国家自然科学基金面上项目。
胡江胜,2013年6月毕业于南京大学数学系,获理学博士学位,主要从事同调代数与代数表示理论等领域的研究,研究内容涉及逼近理论、高维同调理论、Gorenstein同调理论与复形的相对上同调理论等。现任江苏理工学院教授,江苏省“333工程”第三层次培养对象,江苏高校“青蓝工程”优秀青年骨干教师。近年来在《Israel J. Math.》《Quarterly J. Math.》《J. Algebra》《J. Pure
Appl. Algebra》《Sci. China Math.》等国际SCI期刊上发表学术论文30余篇。先后主持国家自然科学基金面上项目、天元项目、青年项目和江苏省自然科学基金面上项目等课题。
朱荣民,华侨大学博士,2021年在南京大学获得博士学位,在2018年12月至2020年11月间,在捷克布拉格查理大学联合培养。研究方向为同调代数与代数表示论,在Publ.Math.Debrecen、Comm Algebra、J.Algebra Appl.等期刊发表SCI论文。
撰稿:王永铎;终审:刘全恩。
 甘公网安备62010302000688号
甘公网安备62010302000688号 


